《数据密集型应用系统设计》第3章-数据存储与检索
OLTP和OLAP
二者区别如下:
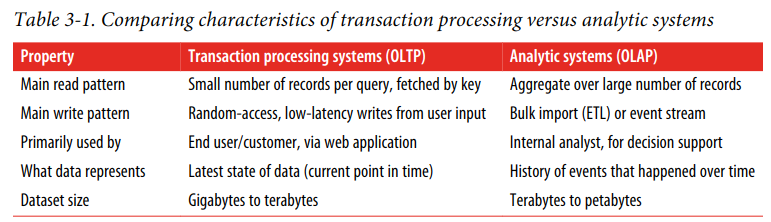
正是这些区别,导致了它们存储格式的不同。
OLTP的存储格式
从最简单的说起
一个基本的索引 + 磁盘存储
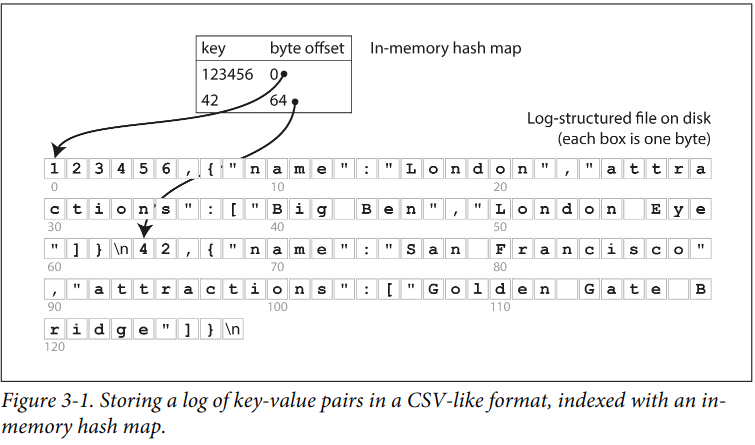
优化存储占用 - 压缩
丢弃重复的key,每个key只保留最新的值:

但是上面这种结构有以下缺点:
- 哈希索引必须全部放入内存,因为磁盘上的哈希索引需要大量的随机IO。
- 区间查询效率不高,只能逐个查询。
这些问题将由下面的存储结构解决。
SSTables和LSM-Tree
SSTables
排序字符串表,每个key在每个合并的段文件中只能出现一次。它的段文件合并过程与内存索引如下:

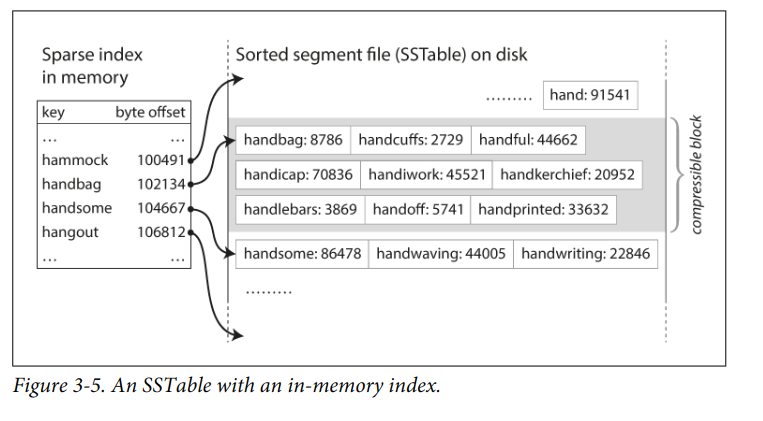
LSM-Tree的引入
SSTables的读取已在上面讲过,那写入呢,写入可能以任意顺序出现,该如何让数据排序呢?一般流程如下:
- 先写入内存中的平衡树结构中,比如红黑树或者AVL树,此结构被称为内存表。
- 内存表达到某个阈值时,将其作为SSTables文件写入磁盘,阈值一般为几兆。因为内存表是有序的,所以写入磁盘很高效。
- 读请求,先读内存表,找不到,就再读最新的磁盘段文件,然后再读次新的段文件,以此类推。
- 后台进程周期性执行合并与压缩。
- 为了防止崩溃丢失数据,还会引入一个日志文件,以记录每个写入。
上面这个思路被称为Log-Structured Merge-Tree,即LSM-Tree。LevelDB、RocksDB、Cassandra、HBase等都采用了类似的技术。
LSM-Tree的优化
查找一个不存在的key会很慢,看上面的第3点。所以引入布隆过滤器,当key不存在时,能很快得出结果。
B-Tree
B-Tree将数据库分解为固定大小的页,一般为4K,和底层磁盘的页大小相适配。一个页面由以下数据组成:
- 若干个key,key是连续的
- 对子页的引用
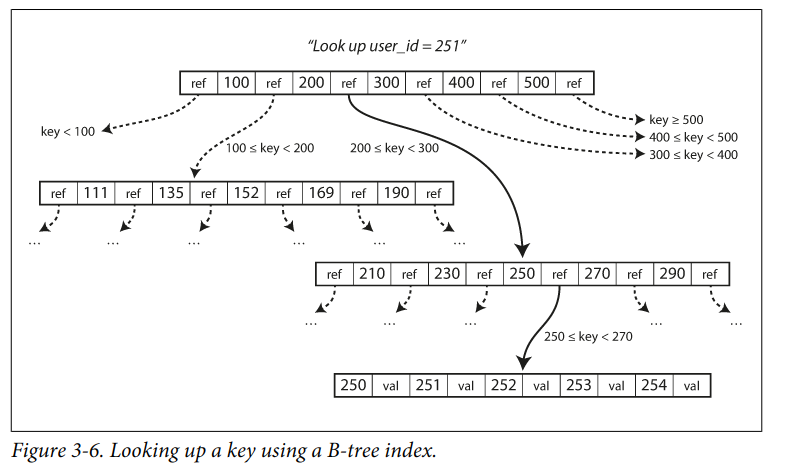
一个页所引用的子页个数称为分支因子, $ n $个key的B-Tree深度为 $O(log n)$。4层、分支因子为500、页大小为4K的B-Tree就可以存储256TB的数据。
B-Tree的增删改查
上面已经说过查询了,改数据也比较容易,先查到页,更改,再写入。增加新key,也是先查到页,添加key,如果页容量不够的话,则可能涉及到页的分裂:
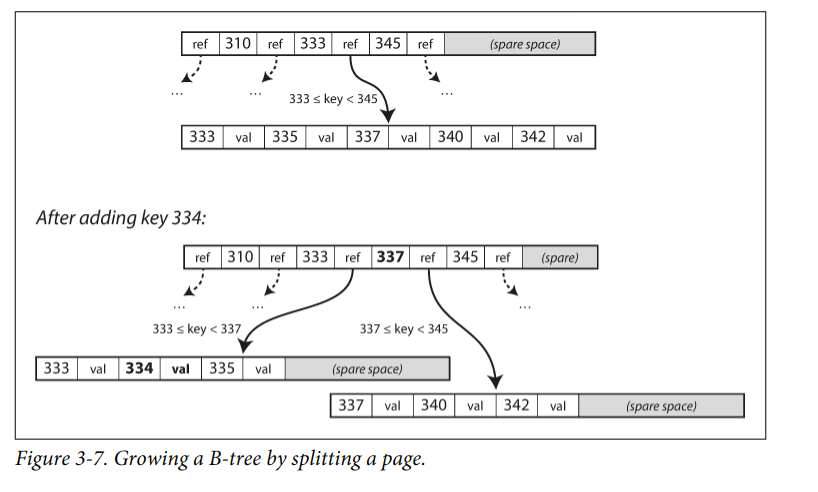
删除则更复杂了,详见《算法导论》的18.3节。同样地,为了防止崩溃导致数据丢失,会引入一个日志文件,以记录每个写入,称为write-ahead log(WAL),也被称为预写日志、重做日志。
B-Tree的几种优化
- 写时复制,COW。
- B+Tree,叶子节点存储数据,其他的节点只存key,以节省页空间,增加分支因子,减少层数。叶子节点增加对左右兄弟的引用,这样范围查询时就不用再跳回父页了。
B-Tree和LSM-Tree对比
写放大:一次数据库写入导致多次磁盘写。
- LSM-Tree的写放大比B-Tree要来的小,因为LSM-Tree顺序写入紧凑的SSTable文件。
- B-Tree必须至少写两次,一次写入预写日志,一次写入树的页本身。MySQL InnoDB甚至存在Double Write,即同一页写两次。
- LSM-Tree对压缩支持更好,存储开销更小。
- 虽然LSM-Tree对压缩支持更好,但带来的副作用是:高吞吐量写入时,磁盘带宽被压缩和写入共享。
- B-Tree提供强大的事务语义,事务隔离通常以在key范围内加锁来实现。
OLAP的存储格式
数据仓库:使用单独的数据库(数据仓库)进行分析,而不是在OLTP系统上。
ETL:Extract-Transform-Load,即将数据导入数据仓库的过程。
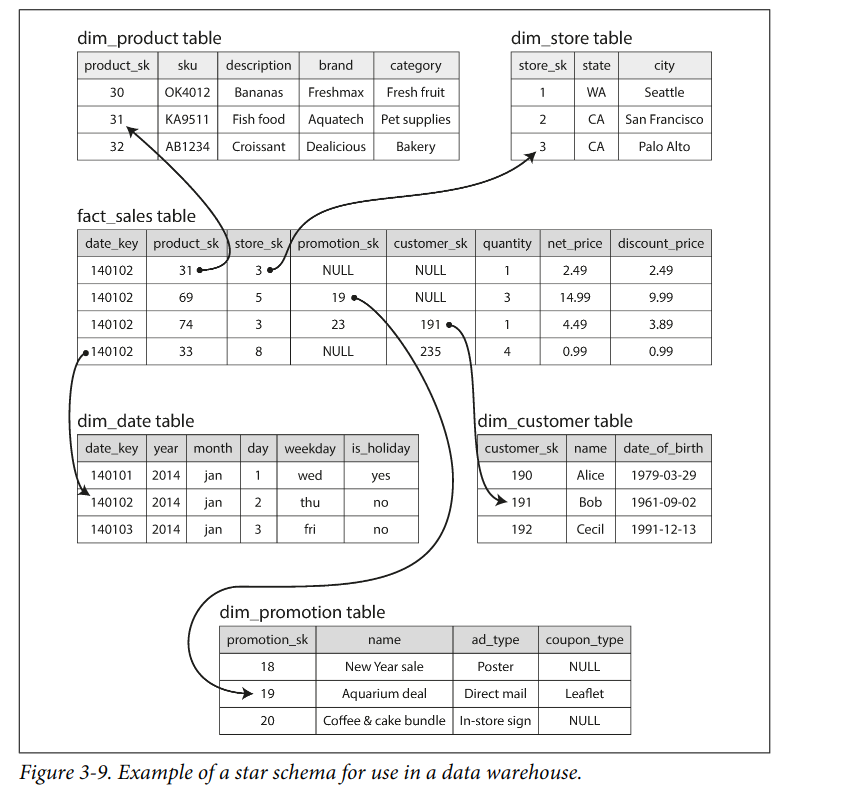
星型分析模式
事实表在中间,通过外键与维度表关联,仿佛星星一样,因而得名。
雪花型分析模式
雪花型分析是在星型分析基础上更进一步,即维度表还可以再关联子维度表,这样形成一个雪花图案。
列式存储
引入的目的
行存储不利于OLAP,事实表一般有几百列,而分析往往只需要几列。如果采用行存储,仍需将所有行查出来,然后过滤。而列存储可以高效地支持此种查询:
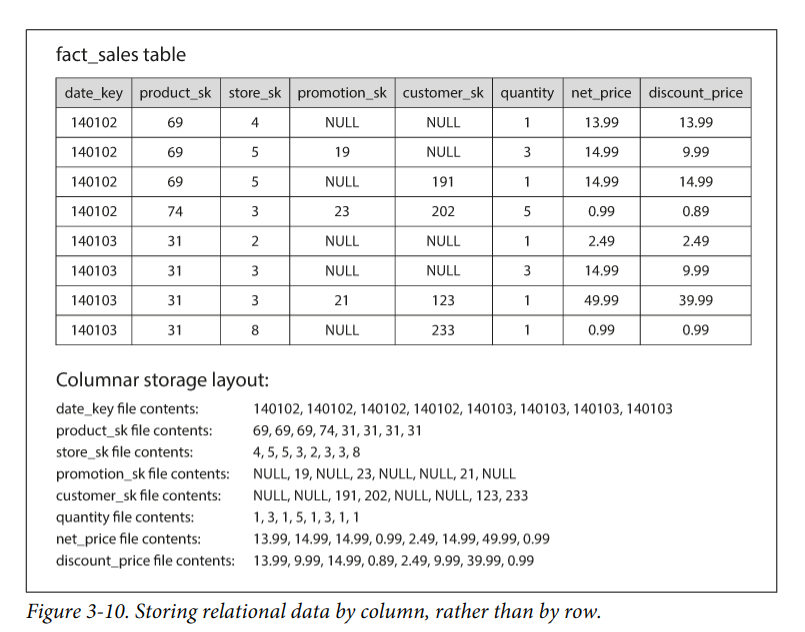
每个列文件以相同的顺序保存数据行,读哪一列,直接读取文件即可。而且可以很方便的以相同的偏移量读取行。
列压缩
引入bitmap进行压缩:

物化视图
实际查询结果的副本,并被写入磁盘。当底层数据发生变化时,物化视图也需要更新,但这种更新会影响写入性能,所以一般在读密集的OLAP场景中用的多。物化视图的一个特例是OLAP立方体,它是由不同维度组合的网格:
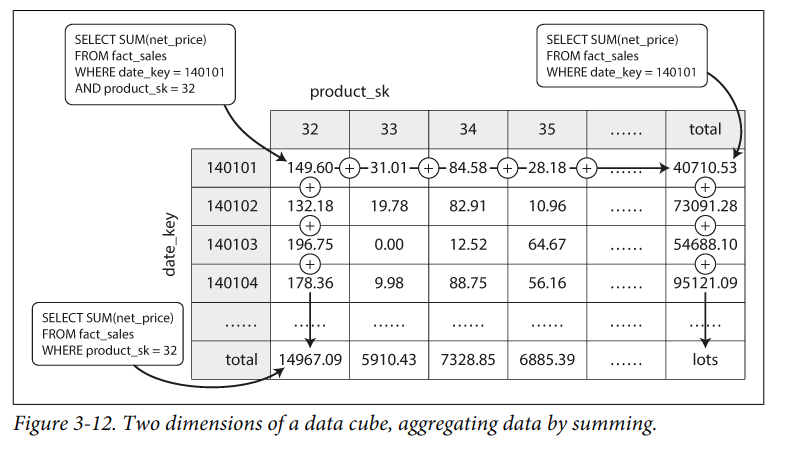
OLAP立方体可以推广到 $n$ 维,比如:日期、产品、商店、客户。